Octahedral Encoding

The Physically Based Rendering 4th Edition book’s section on Octahedral Encoding shares an algorithm, but less of the intuition than I needed. Here’s what I’ve figured out.

Dividing a vector by its L1 norm yields a vector whose L1 norm equals 1. #

Octahedral encoding operates on unit vectors, i.e. vectors with $v_x^2 + v_y^2 + v_z^2 = 1$. To encode a vector with octahedral encoding, we first divide the vector by its L1 norm, $|v_x| + |v_y| + |v_z|$.

This yields a vector whose L1 norm equals 1:

The following two images graphically depict the domain and range respectively, in 2D.

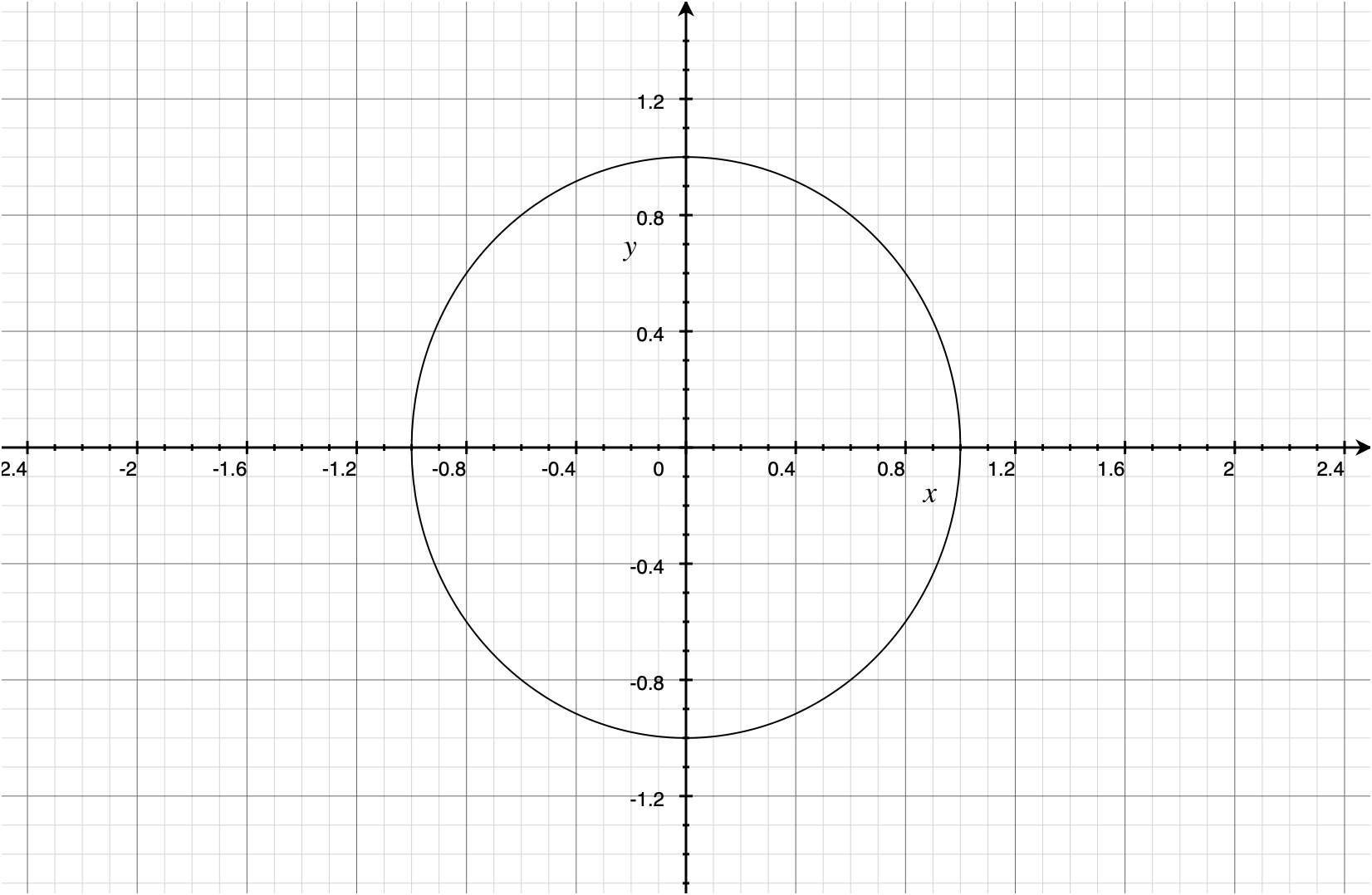
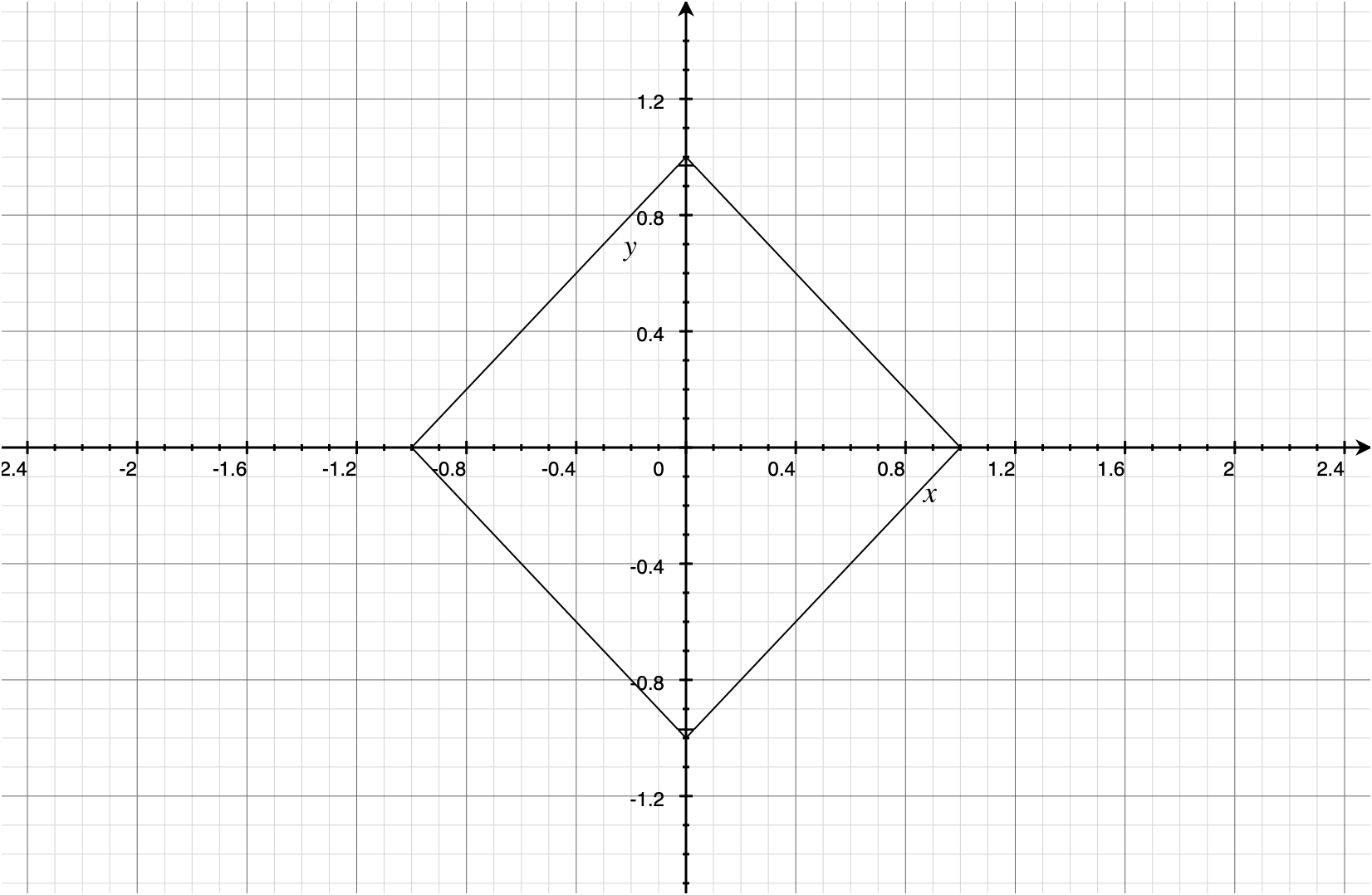
Dividing a vector by its L1 norm is invertible by normalizing. #

We’ve performed a scalar multiplication that makes our L1 norm equal 1, thus decoding is a scalar multiplication by the reciprocal, and makes our L2 norm equal 1. This happens to be the normalize operator.

One of the vector’s components conveys only 1 bit of information. #

Knowing the norm, we can derive the third component from the other two, with the exception of its sign. That is, if the L1 norm equals 1, then $|v_z| = 1 - |v_x| - |v_y|$, and $v_z = |v_z|$ or $v_z = -|v_z|$.

Omitting a component yields a 2D vector whose L1 norm $\leq$ 1. #

The L1 norm of the 3D vector was $|v_x| + |v_y| + |v_z| = 1$. Subtracting $v_z$ or any other component from both sides yields $|v_x| + |v_y| = 1 - |v_z|$, where $|v_z|$ has effectively become a slack variable. Thus $|v_x| + |v_y| \leq 1$.

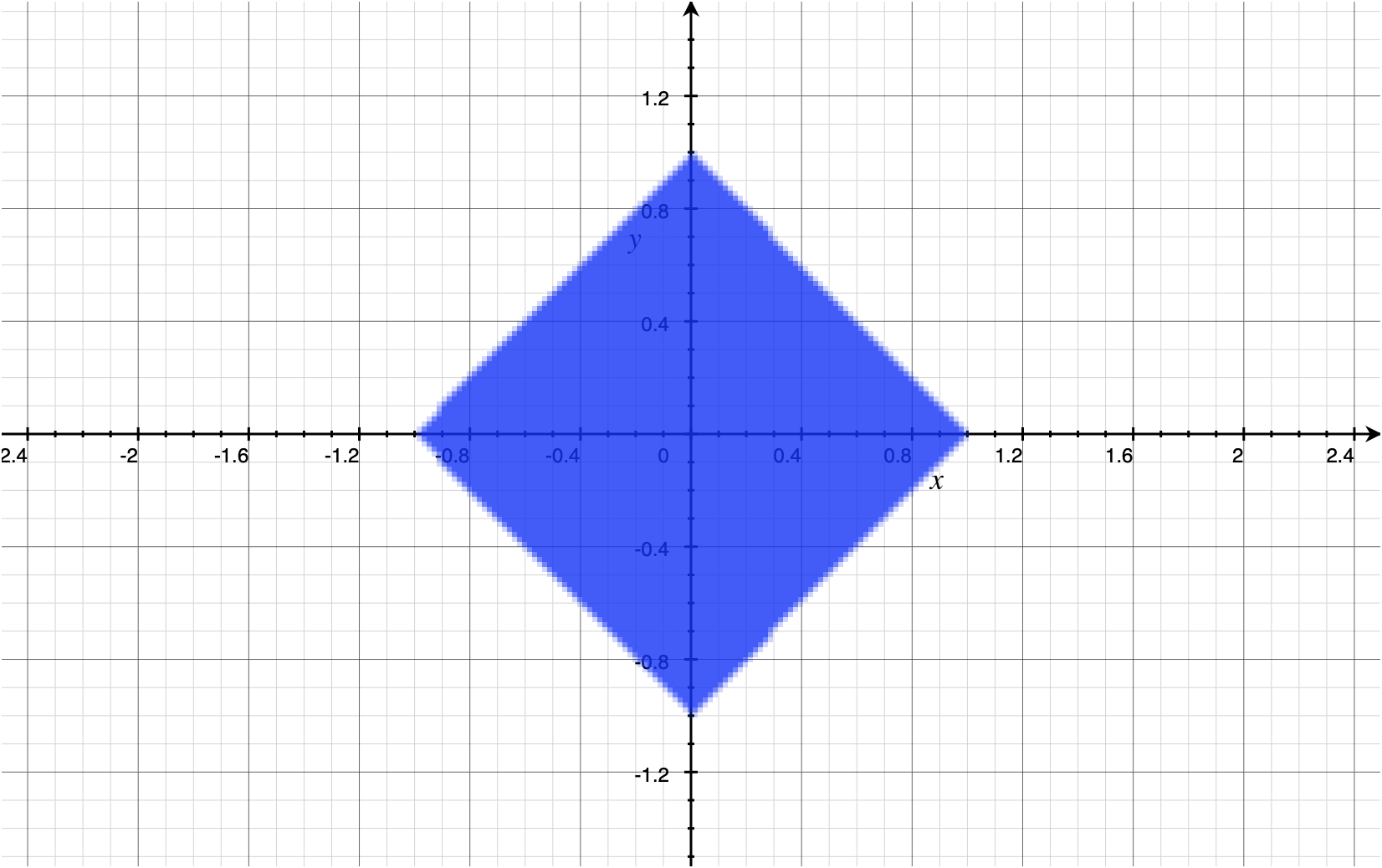
A 2D vector whose L1 norm $<$ 1 only uses half of the available storage. #

Our 2D vector is comprised of two components, each in $[0, 1]$. However, $|v_x| + |v_y| < 1$. In the image below, note the area occupied by the blue diamond relative to the area from (-1, -1) to (1, 1).

We can show that half of the storage is unused by construction. The vector $v' = \operatorname{sign}(v) - v$ yields another vector with $|v'_x| + |v'_y| \geq 1$, where $\operatorname{sign}$ is defined component-wise the same as C++’s copysign with a magnitude of 1.

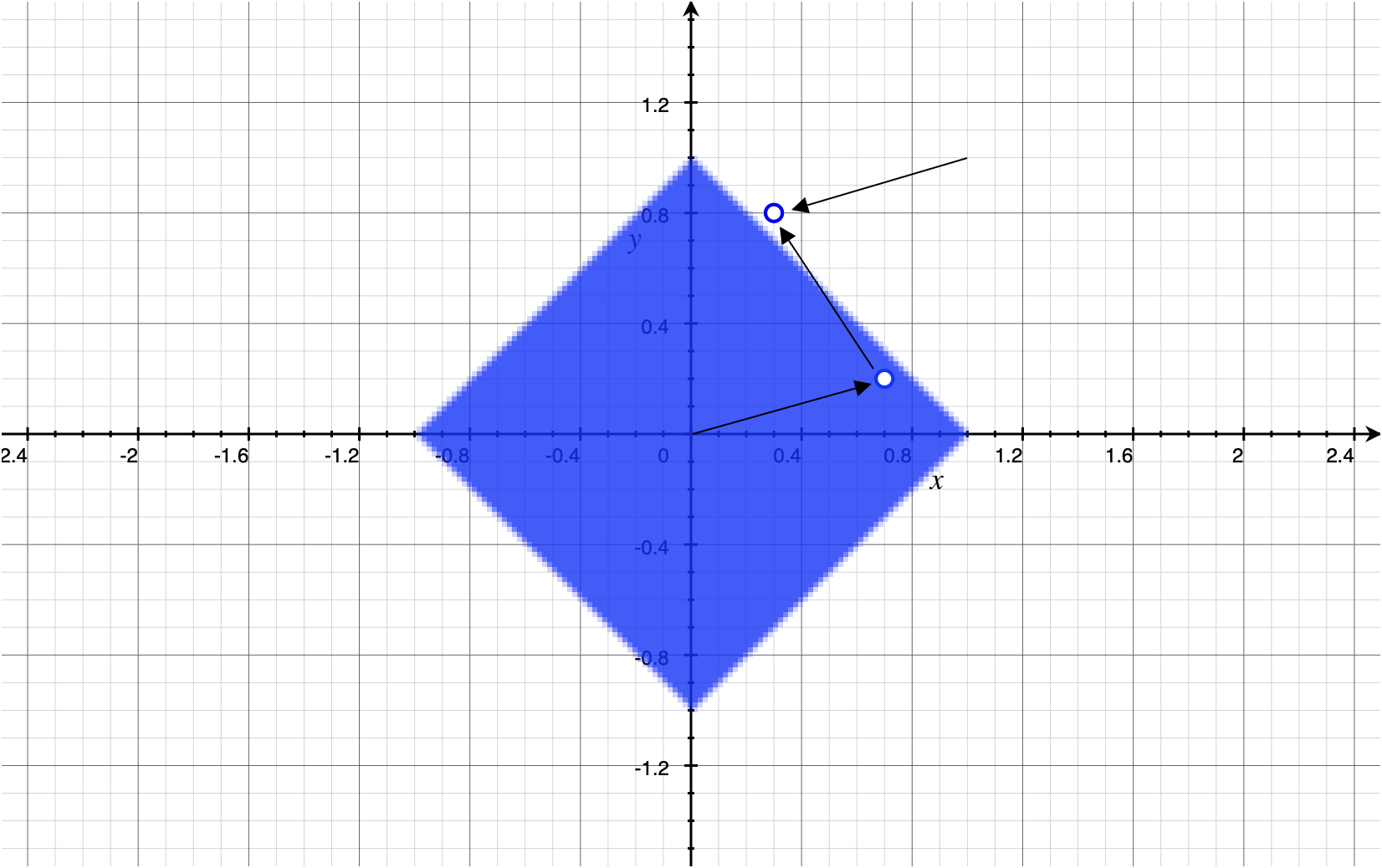
Note that we’re talking about L1 norm $<$ 1 and not L1 norm $\leq$ 1. We have $v = v'$ when $|v_x| + |v_y| = 1$, so we’ll take that as a special case and reason carefully about it.

We encode the third component’s sign by the 2D vector’s L1 norm. #

Using the vector $v'$ as defined in the previous section, we can encode $v$ as

This gives us the sign of $v_z$.

Swap the x and y coordinates so $v = v'$ when L1 norm equals 1. #

Let $v$ be a vector whose L1 norm equals 1, and $v' = \operatorname{sign}(v) - v$. If $v$ is (0, 1), then $v'$ is (1, 0). If $v$ is (-1, 0), then $v'$ is (0, 1).

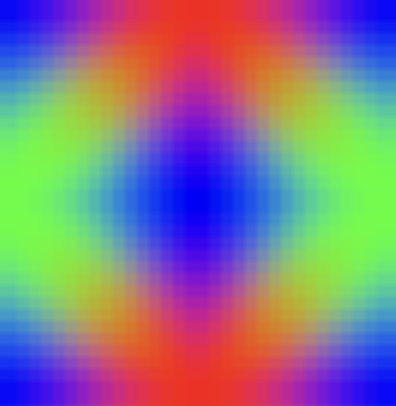
Using octahedral encoding with $v'$ as defined above to encode a gradient shows what the problem is. We have finite resolution and the case where L1 norm equals 1 creates a discontinuity.

Now let’s redefine $v'$ as $v' = (1 - abs(v.yx)) * \operatorname{sign}(v)$. If $v$ is (0, 1), then $v'$ is (0, 1). If $v$ is (-1, 0), then $v'$ is (-1, 0).

Swapping the x and y coordinates, $v_z = +0$ and $v_z = -0$ no longer puts us on either side of a discontinuity, we see a smooth gradient.

Algorithm #

// Define our own 'sign' function to match copysign semantics.
// The result shouldn't be zero since this changes the L1 norm.
vec2 sign2(float x) {
    return x >= 0.0 ? 1.0 : -1.0;
}
vec2 sign2_vec2(vec2 v) {
    return vec2(sign_correct(v.x), sign2(v.y));
}

vec2 swap(vec2 v) {
	return (1 - abs(u.yx)) * sign2_vec2(u);
}
vec2 enc(vec3 v) {
    vec2 u = v.xy / (abs(v.x) + abs(v.y) + abs(v.z));
    return v.z >= 0.0 ? u : swap(u.yx);
}
vec3 dec(vec2 u) {
    float z = 1.0 - abs(v.x) - abs(v.y);
    return normalize(vec3(z >= 0.0 ? u : swap(u.yx), z));
}